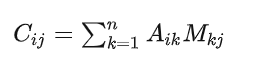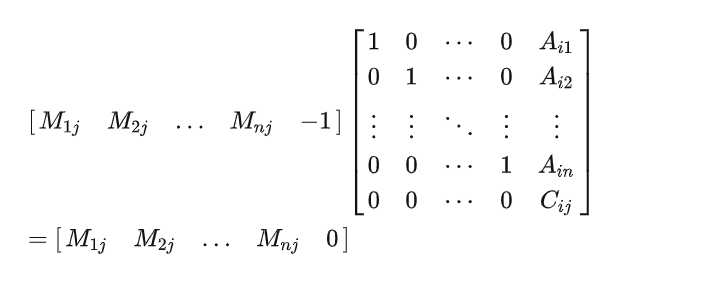一、格的概述

zvmT54.png

格是离散的Rn加子群。每个格都是一些线性无关的向量产生的集合，称之为基。

二、格基规约

任意格都有无数个基，LLL 算法就是在格上找到一组基：其长度尽可能最小，并于基中其他矢量尽可能正交。即对应方程组中找到一组满足等式的最优解。

规约算法过程太过复杂，此处省略。。。

三、格基规约简单使用

1.对二元单方程的求解

题目：

1
2
t = 44,P,Q已知，求解p，q
t=(p*P-58*P+q)%Q

格的构造：

zvmoaF.png

LLL规约：

1
2
3
4
5
6
7
8
M = Matrix(ZZ, [[1, P],
           [0, Q]])         //在ZZ整数环上定义一个二维矩阵[[1,P],[0,Q]]
v = M.LLL()[0]              //LLL规约

p, q = -v

p = p + 58
q = -q + 44

2.求解矩阵相乘运算中某一未知矩阵

题目描述

题目基于矩阵乘法AM=C，其中这三个均为n×n方阵，M为消息矩阵且较小。

给出矩阵C，并且将A中的随机n个元素毁坏，得到Ac并给出。

试求M。

题目分析：

M为消息矩阵且较小，这意味着我们或许可以从格基规约出发。

首先，C中的一个元素Cij可以看成是A的第i行的行向量和M的第j列的列向量作内积而得到的，即

zvmIVU.png

因此，一个非常直观的假设就是，假设存在i，使得A的第i行的行向量未被毁坏的话，我们就能利用该行向量，和M的所有列向量作内积，得到C的第i行结果。在此基础上，便可以构造格

zvm4bT.png

如果能够成功规约（最后一个元素为0）的话，我们就能求出消息矩阵M的第j列。然后，遍历所有的j，我们就能求出整个消息矩阵M。

规约：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
C = Matrix(ZZ, C)
Ac = Matrix(ZZ, Ac)

M = [[-1 for j in range(n)] for i in range(n)]

for i in trange(32):
    for j in range(32):
        L = [[0 for j in range(n+1)] for i in range(n+1)]
        for k in range(n):
            L[k][k] = 1
            L[k][n] = Ac[i][k]
        L[n][n] = C[i][j]
        L = Matrix(ZZ, L)
        v = L.LLL()[0]
        if (v[-1] == 0):
            if (v[0] < 0):
                v = -v
            v = v.list()
            for k in range(n):
                M[k][j] = v[k]

print(M)