一、数字签名

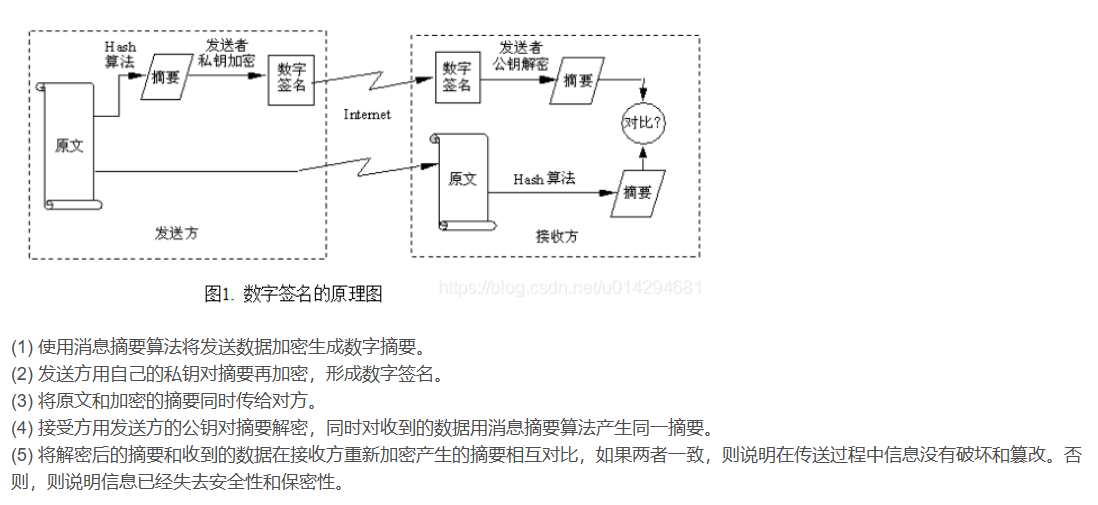
zjZHHg.png

二、DSA介绍

DSA是用于数字签名的算法，基于模算数和离散对数的复杂度。DSA是Schnorr和ElGamal签名方案的变体。

DSA 算法包含了四种操作：密钥生成、密钥分发、签名、验证

1、密钥生成

密钥生成包含两个阶段。第一阶段是算法参数的选择，可以在系统的不同用户之间共享，而第二阶段则为每个用户计算独立的密钥组合。

pCa8ppq.png

2、密钥分发

签名者需要透过可信任的管道发布公钥 y，并且安全地保护 x 不被其他人知道。

3、签名流程

pCa3zhn.png

4、验证签名

pCa8910.png

三、DSA解密

1.已知 k：

如果知道了随机密钥 k，那么我们就可以根据

s ≡ (H(m)+xr)k−1modq 计算私钥 x。

这里一般情况下，消息的 hash 值都会给出。

x≡r−1(ks−H(m))modq

2.k 共享

如果在两次签名的过程中共享了 k，我们就可以进行攻击。

假设签名的消息为 m1,m2，显然，两者的 r 的值一样，此外

s1≡(H(m1)+xr)k−1modq

s2≡(H(m2)+xr)k−1modq

这里我们除了 x 和 k 不知道剩下的均知道，那么

s1k≡H(m1)+xr

s2k≡H(m2)+xr

两式相减

k(s1−s2)≡H(m1)−H(m2)modq

此时 即可解出 k，进一步我们可以解出 x。

wp：

1
2
3
4
5
6
7
8
9
10
from Crypto.Util.number import *
import gmpy2
import hashlib
h1,h2,s1,s2,r1,q = [818128692003030167977053277109430684611703076399,486498008062394064249282337122659834542436448201,247121551505513420409531383106944282908920522414,754913008212620944684250081707312932655139381276,1309822693949102705754289540573759976438632888627,1328243644040291196447577554903037460035141284781]
r2 = r1
k = (h1 - h2) * gmpy2.invert(s1 - s2 ,q) % q
flag = (k * s1 - h1) * gmpy2.invert(r1,q) % q
print(flag)
print(long_to_bytes(flag))
print('flag{' + hashlib.md5(str(flag).encode()).hexdigest() + '}')