椭圆曲线：

椭圆曲线加密算法，简称ECC，是基于椭圆曲线数学理论实现的一种非对称加密算法。相比RSA，ECC优势是可以使用更短的密钥，来实现与RSA相当或更高的安全，RSA加密算法也是一种非对称加密算法，在公开密钥加密和电子商业中RSA被广泛使用。据研究，160位ECC加密安全性相当于1024位RSA加密，210位ECC加密安全性相当于2048位RSA加密（有待考证）。

椭圆曲线方程：

椭圆曲线Ep ( a , b ) p为质数，x , y ∈ [ 0 , p − 1 ]

​ y ** 2 = x ** 3 + ax + b (mod p)

表示在p有限域GF(p)上的椭圆曲线方程。

其中，要求曲线是非奇异的（处处可导），有4 a**3 + 27 b * *2 ≠ 0

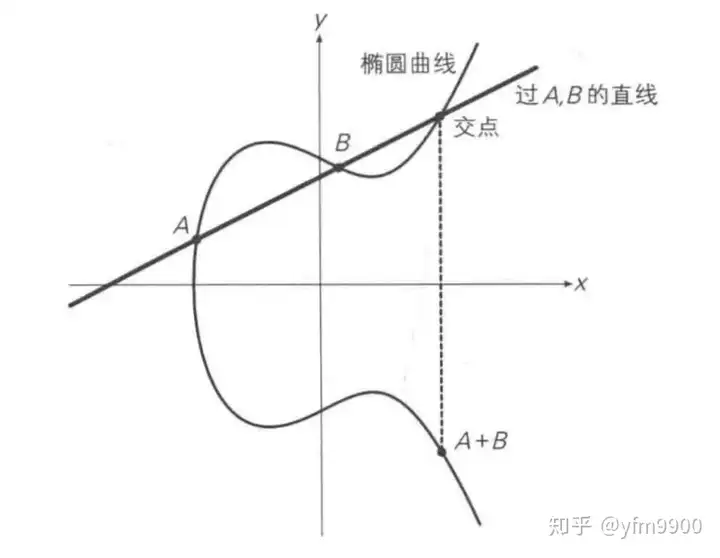
加法运算：

过曲线上的两点A、B画一条直线，找到直线与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A+B，即为加法。如下图所示：A + B = C

img

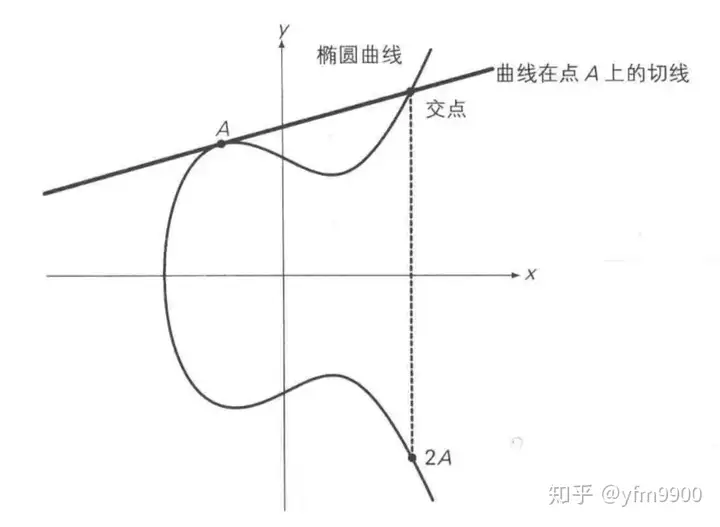
二倍运算

上述方法无法解释A + A，即两点重合的情况，因此在这种情况下，将椭圆曲线在A点的切线，与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A + A，即2A，即为二倍运算。

img

椭圆曲线加密
考虑K = k G ，其中K、G为椭圆曲线Ep(a,b)上的点，n为G的阶（n G = O∞ ），k为小于n的整数。则给定k和G，根据加法法则，计算K很容易但反过来，给定K和G，求k就非常困难。因为实际使用中的ECC原则上把p取得相当大，n也相当大，要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据 。

  • 点G称为基点（base point）
  • k ( k < n ) k(k<n)k(k<n)为私有密钥（private key）
  • K为公开密钥（public key)

下面是利用椭圆曲线进行加密通信的过程：

xbWh7t.png

例题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
p = getPrime(256)
a = getPrime(256)
b = getPrime(256)
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = getPrime(18)
K = k * G
r = getPrime(256)
c1 = m + r * K

c2 = r * G

cipher_left = s2n(flag[:len(flag)//2]) * m[0]   #flag的前半部分乘m[0]，所以只要用密文的除于m[0]即可得到flag前半部分
cipher_right = s2n(flag[len(flag)//2:]) * m[1]   #flag的后半部分点乘m[1]

exp：

已知a，b，G，c1，c2和k的范围(爆破k)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
from tqdm import tqdm

a = 87425770561190618633288232353256495656281438408946725202136726983601884085917
b = 107879772066707091306779801409109036008421651378615140327877558014536331974777
K = (49293150360761418309411209621405185437426003792008480206387047056777011104939 , 43598371886286324285673726736628847559547403221353820773139325027318579443479)
G = (34031022567935512558184471533035716554557378321289293120392294258731566673565 , 74331715224220154299708533566163247663094029276428146274456519014761122295496)
#私钥k小于1000000
c1 = (3315847183153421424358678117707706758962521458183324187760613108746362414091 , 61422809633368910312843316855658127170184420570309973276760547643460231548014)
c2 = (12838481482175070256758359669437500951915904121998959094172291545942862161864 , 60841550842604234546787351747017749679783606696419878692095419214989669624971)
cipher_left = 75142205156781095042041227504637709079517729950375899059488581605798510465939
cipher_right = 61560856815190247060747741878070276409743228362585436028144398174723191051815

f1 = c1[0]^3 + a*c1[0] + b - c1[1]^2 
f2 = G[0]^3 + a*G[0] + b - G[1]^2
p = GCD(f1,f2)
print(p)  
print(isPrime(p))

E = EllipticCurve(GF(p),[a,b])
c1 = E(c1)
c2 = E(c2)
ks = primes(2^17,2^19)
for k in tqdm(ks):
    tmp = k*c2
    m = c1 - tmp
    m0 = cipher_left*inverse_mod(int(m[0]),p)%p
    m0 = long_to_bytes(m0)
    if b'flag' in m0:
        print(m0+long_to_bytes(cipher_right*inverse_mod(int(m[1]),p)%p))
        break