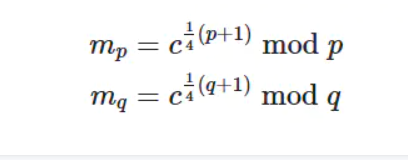公钥指数e的相关攻击

1.小公钥指数攻击

可攻击特征:

e 特别小，比如 e 为 3。

加密分析：

e=3, 公钥中的加密指数e很小，但是模数n很大
有RSA加密公式： C=M^e % n (C密文，M明文)
则：

  • 当M^e < n 时，
    C = M^e ，所以对C开方就能得到M

  • 当M^e ＞ n 时，此时用爆破的方法
    假设我们　 Ｍ^e / n 的商为 k 余数为C，
    则Ｍ^e = kn + C，对K进行爆破，只要k满足 kn + C能够开e次方就可以得明文

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from gmpy2 import iroot
import libnum
e = 0x3
n = 
c = 

k = 0
while 1:
    res = gmpy2.iroot(c+k*n,e)  #c+k*n 开3次方根 能开3次方即可
    #print(res)
    #res = (mpz(13040004482819713819817340524563023159919305047824600478799740488797710355579494486728991357), True)
    if(res[1] == True):
        print(libnum.n2s(int(res[0]))) #转为字符串
        break
    k=k+1

2.小公钥指数攻击之Rabin 算法:

可攻击特征:

Rabin 算法的特征在于 e=2（并且一个密文可以对应多个明文）

攻击原理:

7EIxTx.png

如果p,q是形为4k+3的不同素数(p≡q≡3(mod4)),则

​ 7ETA8U.png

解题脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
c = int(open('flag.enc','r').read().encode('hex'),16)
#print c
 
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
n = p*q
 
mp = pow(c,(p+1)/4,p)
mq = pow(c,(q+1)/4,q)
yp = gmpy.invert(p,q)
yq = gmpy.invert(q,p)
 
a = (yp*p*mq + yq*q*mp)%n
b = n - int(a)
c = (yp*p*mq - yq*q*mp)%n
d = n - int(c)

#a，b，c，d这四个值之一是原始明文m mm，但是如果没有其他信息，就无法确定这四个是正确的。

三个素数的rabin：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#n是因数的集合[p,q,r]
N = 1 
for p in n: 
    N *= p 
 
def crt(primes, remainders): 
    result = 0 
    for i in range(len(primes)): 
        Mi = N // primes[i] 
        inv = inverse(Mi, primes[i]) 
        result += remainders[i] * Mi * inv 
    return result % N 
 
 
roots = [pow(c, (int(p) + 1) // 4, int(p)) for p in n] 
 
# 遍历所有可能的符号组合 
for signs in itertools.product([1, -1], repeat=3): 
    adjusted_roots = [ 
        signs[0] * roots[0] % n[0], 
        signs[1] * roots[1] % n[1], 
        signs[2] * roots[2] % n[2] 
    ] 
    flag = crt(n, adjusted_roots) 
    print(long_to_bytes(flag))

3.低加密指数广播攻击:

介绍

如果选取的加密指数较低，并且使用了相同的加密指数给一个接受者的群发送相同的信息，那么可以进行广播攻击得到明文。选取了相同的加密指数 e（这里取 e=3），对相同的明文 m 进行了加密并进行了消息的传递，那么有：

c1 ≡ m^e mod n1

c2 ≡ m^e mod n2

c3 ≡ m^e mod n3

对上述等式运用中国剩余定理，在 e=3 时，可以得到：

cx ≡ m^3 mod n1n2n3

通过对 cx 进行三次开方就可以求得明文

1
2
3
4
5
6
7
from xenny.ctf.crypto.modern.asymmetric.rsa.lowe_broadcast import attack
from Crypto.Util.number import long_to_bytes

n_list = 
c_list = 

print(long_to_bytes(attack(n_list=n_list, c_list=c_list, e=3)[0]))   //开三次方

4.离散对数求e

m ** e % n = c

1
e = sympy.discrete_log(n,c1,m)