Crypto-streamgame系列题目: 首先给出大佬博客链接:(32条消息) streamgame系列的总结_T1an5t的博客-CSDN博客_streamgame2
题目:streamgame1,来源:2018强网杯: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 from flag import flagassert flag.startswith("flag{" )assert flag.endswith("}" )assert len (flag)==25 def lfsr (R,mask ): output = (R << 1 ) & 0xffffff i=(R&mask)&0xffffff lastbit=0 while i!=0 : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) R=int (flag[5 :-1 ],2 ) mask = 0b1010011000100011100 f=open ("key" ,"ab" ) for i in range (12 ): tmp=0 for j in range (8 ): (R,out)=lfsr(R,mask) tmp=(tmp << 1 )^out f.write(chr (tmp)) f.close()
1.先阅读代码,前面是对flag的一些限制,我们可以得到的信息:导入flag(废话,当然不能直接给你),flag的形式是flag{*****},括号内总长度19
1.先阅读代码,前面是对flag的一些限制,我们可以得到的信息:导入flag(废话,当然不能直接给你),flag的形式是flag{****},括号内总长度19
2.然后是加密函数lfsr,我们现在并不想知道他是什么,好的,那么我们记住它是加密函数就行了,往下看
3.R取了flag中间部分并且以二进制形式转换为数字,那么我们就知道了flag括号内的东西一定是0或者1,我们可以调出idle测试一下:
4.到这里我们可以得到的结论:flag一共19位(不含开头结尾,以下都是),且是由0和1组合而成
5.然后我们再看这段把结果写入key文件的函数
1 2 3 4 5 6 7 8 9 10 mask = 0b1010011000100011100 f=open ("key" ,"ab" ) for i in range (12 ): tmp=0 for j in range (8 ): (R,out)=lfsr(R,mask) tmp=(tmp << 1 )^out f.write(chr (tmp)) f.close()
其实就是每次宣进行对mask和R作用加密函数并生成新的R同时得到1bit数据,然后每8bit数据转化成一个对应的ascii再写入key文件中,一共写入了12个字节,
6.这里我们已经磨磨唧唧的分析完了程序的大致思路了,除了lfsr这个加密函数没有解决。针对这道题,我们对付它的方法是不解决!我们上面4说过,flag19位,而且不是0就是1,那么一共会有 2**19 种可能,也就是524288种情况,那就…密码学绝学—爆破大法,这里爆破脚本偷自https://blog.csdn.net/qq_38412357/article/details/79696263:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 def lfsr (R,mask ): output = (R << 1 ) &0xffffff i=(R&mask)&0xffffff lastbit=0 while i!=0 : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) key=[85 ,56 ,247 ,66 ,193 ,13 ,178 ,199 ,237 ,224 ,36 ,58 ] mask=0b1010011000100011100 for k in range (2 **19 ): R=k; a='' judge=1 for i in range (12 ): tmp = 0 for j in range (8 ): (k, out) = lfsr(k, mask) tmp = (tmp << 1 ) ^ out if (key[i]!=tmp): judge=0 break if (judge==1 ): print 'flag{' +bin (R)[2 :]+'}' break
题目:streamgame2,来源:2018强网杯: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 from flag import flagassert flag.startswith("flag{" )assert flag.endswith("}" )assert len (flag)==27 def lfsr (R,mask ): output = (R << 1 ) & 0xffffff i=(R&mask)&0xffffff lastbit=0 while i!=0 : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) R=int (flag[5 :-1 ],2 ) mask=0x100002 f=open ("key" ,"ab" ) for i in range (12 ): tmp=0 for j in range (8 ): (R,out)=lfsr(R,mask) tmp=(tmp << 1 )^out f.write(chr (tmp)) f.close()
1.代码我就不再具体分析了,跟1基本一致,只是key是另一个文件,flag的位数变成了21位而已,所以会有2**21 种可能 ,也就是2097152种,可以继续爆破。把1的脚本中的key和mask改成对应数值,range()改成2的二十一次方即可。
最后得到:flag{110111100101001101001}
题目:streamgame4,来源:2018强网杯: 1.为什么是4,不是3呢,因为3才是我们认为最难的。会放在最最最后面说。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 from flag import flagassert flag.startswith("flag{" )assert flag.endswith("}" )assert len (flag)==27 def nlfsr (R,mask ): output = (R << 1 ) & 0xffffff i=(R&mask)&0xffffff lastbit=0 changesign=True while i!=0 : if changesign: lastbit &= (i & 1 ) changesign=False else : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) R=int (flag[5 :-1 ],2 ) mask=0b110110011011001101110 f=open ("key" ,"ab" ) for i in range (1024 *1024 ): tmp=0 for j in range (8 ): (R,out)=nlfsr(R,mask) tmp=(tmp << 1 )^out f.write(chr (tmp)) f.close()
1024字节,这极大地增大了我们的爆破难度。
但是…我们还是不需要去了解加密函数内部到底发生了什么。继续爆破,因为加密的复杂性,所以key即便我们只取前几个,重复率也很低,所以我们取前5个字节就可以了,脚本依然偷自https://blog.csdn.net/qq_38412357/article/details/79696263:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 key=[209 ,217 ,64 ,67 ,147 ] def nlfsr (R,mask ): output = (R << 1 ) &0xffffff i=(R&mask)&0xffffff lastbit=0 changesign=True while i!=0 : if changesign: lastbit &= (i & 1 ) changesign=False else : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) mask=0b110110011011001101110 for k in range (2 **21 ): R=k; a='' judge=1 for i in range (5 ): tmp=0 for j in range (8 ): (k,out)=nlfsr(k,mask) tmp=(tmp << 1 )^out if (key[i] != tmp): judge = 0 break if (judge==1 ): print 'flag{' +bin (R)[2 :]+'}' break
题目:streamgamex,来源:2018HITB-XCTF: 1.打过QWB的师傅肯定上面一眼带过,因为其实大多数都是这么做的,下面会慢慢有所不同,希望你能坚持看下去。
我们来看看这个streamgame5把:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 from flag import flagassert flag.startswith("flag{" )assert flag.endswith("}" )assert len (flag)==47 def lfsr (R,mask ): output = (R << 1 ) & 0xffffff i=(R&mask)&0xffffff lastbit=0 while i!=0 : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) R=int (flag[5 :-1 ],2 ) mask = 0b10110110110011010111001101011010101011011 f=open ("key" ,"ab" ) for i in range (64 ): tmp=0 for j in range (8 ): (R,out)=lfsr(R,mask) tmp=(tmp << 1 )^out f.write(chr (tmp)) f.close()
题目描述:
hashlib.sha256(flag).hexdigest()==b2dcba51efd4a7d6157c956884a15934cb3edd3d2c1026830afa8db4ec108b58
2.熟悉的配方,不一样的味道。成了,依然是01的组合,flag长度41位,爆破空间2**41 共 2199023255552 两万亿次,若您挖矿隐居来打CTF或者手握美帝顶级超计的话,请使用上面提供的爆破脚本即可!!
3.那么这回我们来了解了解lfsr这个加密函数究竟干了什么吧:
首先百度关键字lfsr来看看,大多的答案都是这样的:
LFSR(Linear Feedback Shift Register )翻译成中文就是线性反馈移位寄存器。其反馈函数是寄存器中的某些位的简单异或,这些位也称之为抽头序列。一个N位的LFSR能够在重复之前产生2^N-1位长的伪随机序列。只有具有一定抽头序列的LFSR才能通过所有2^N-1个内部状态,产生2^N-1位长的伪随机序列,这个输出的序列就称之为M序列。
4.好,看了上面这个lfsr的描述之后,我相信你差不多还是没懂。那么我以streamgame1的程序来举例(请一边看着1的源码一边食用以下内容!):
1 2 3 4 5 6 7 8 9 def lfsr (R,mask ): output = (R << 1 ) & 0xffffff i=(R&mask)&0xffffff lastbit=0 while i!=0 : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit)
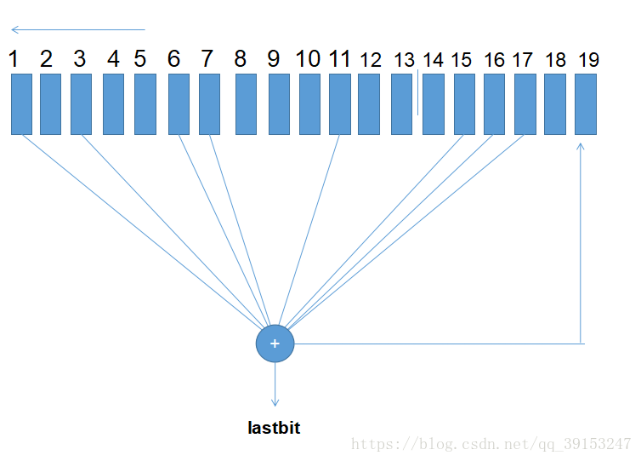
①.output等于传入的R左移1bit然后和0xffffff进行与操作,也就是相当于保留了低24bit
②.i等于R与mask进行与操作再与0xffffff进行与操作,相当于保留了低24bit位上mask掩码对应的位置(学过计算机网络的话可能对我说的掩码这种说法有一个更好的理解),也就是说mask上为1的bit位才会被保留,其余位置全都是0。
③.while循环里面每次lastbit要异或i与1与操作后的结果,然后每次i右移1bit直至为0。跟②结合在一起看的话,就相当于mask中为1的位置取出来一起进行了异或操作然后返回结果。
④.最后output要异或上lastbit,结合①来看这就相当于传入的R左移1bit后将③中i的结果保存在了R最低bit位并把这个新的R返回;lastbit作为我们要写入的key中的第一个bit返回。
坚持看完上面这段又臭又硬的话之后再来结合掩码mask看看下面我画的这张图你大概就能明白到底是怎么一回事了
1 mask = 0b1010011000100011100
5.这回我们再回归到streamgamex,我们可以清晰地看到它的lfsr函数中output以及i的初始化中都要和0xffffff进行与运算,那么结合我们上面的学习就可以知道,我们传入的R只有低24bit位会影响最后的key值,所以只需爆破这24bit位,再根据题目描述的hash值来确定其余的17bit即可!
题目:oldstreamgame,来源:2018CISCN: 1.到上面为止,我们基本摸清了lfsr的思路,但是我们的思维还是没有突破,翻来覆去的就是爆破。那么这次碰到的这个题就不再是了!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 flag = "flag{xxxxxxxxxxxxxxxx}" assert flag.startswith("flag{" )assert flag.endswith("}" )assert len (flag)==14 def lfsr (R,mask ): output = (R << 1 ) & 0xffffffff i=(R&mask)&0xffffffff lastbit=0 while i!=0 : lastbit^=(i&1 ) i=i>>1 output^=lastbit return (output,lastbit) R=int (flag[5 :-1 ],16 ) mask = 0b10100100000010000000100010010100 f=open ("key" ,"w" ) for i in range (100 ): tmp=0 for j in range (8 ): (R,out)=lfsr(R,mask) tmp=(tmp << 1 )^out f.write(chr (tmp)) f.close()
2.mask和lfsr中的与运算都有了严格的限制,根据描述可以看到flag是8个16进制数,也就是32位的二进制, 2**32=4294967296。看了一些wp好像还真有多线程暴力大法出来的,你们电脑好,我服气!
3.鉴于本人电脑小霸王起步,还想在规定时间内求出结果,那么只好再深入的研究一下这个算法了。画出它的流程图:
4.根据这张特别丑的图,我们可以看出,随着不断的左移,慢慢的,后面生成的bit位的key的结果会由key前面bit位来异或产生。那么我们考虑这么一种极限情况,当flag的第32位处于图中1的位置时,其后的31位是不是就都为key中对应的值了,然后这个运算就变成了flag的最后一位与前31位的key选取mask对应位置来异或运算后可以得到第32位key的结果,根据异或运算的性质,我们就可以得出flag的最后一位=前32位的key对应mask的位置的异或运算的结果。然后我们这些bit右移一位,那么flag的倒数第二位就同样可以求出来。以此类推,我们就可以在32次异或运算中求出整个flag,一秒出答案!
5.放出脚本:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 key = "00100000111111011110111011111000" fkey=key i=1 tmp = "" while True : res = int (fkey[i])^int (fkey[i+3 ])^int (fkey[i+10 ])^int (fkey[i+18 ])^int (fkey[i+22 ])^int (fkey[i+25 ])^int (fkey[i+27 ])^int (fkey[i+30 ]) i -= 1 tmp = str (res) + tmp fkey = key + tmp if len (fkey) == 64 : break fkey = fkey[32 :] print "flag{" + hex (int (fkey,2 ))[2 :-1 ] + "}"
脚本可以说非常之丑了,不过逻辑很简单,结合上面的思路很容易看懂。
6.看到这里,其实通过这个再去看上面的124和x,是不是改一改脚本就可以秒出答案了呢!(有兴趣的自己去试试把,这里就不放出这些无意义的代码了,主要是我也没写!)
题目:streamgame3,来源:2018强网杯: 太难了,还没学会,呜呜、、、